Mathématiques et élections
Une loi mathématique, dite loi électorale, permet la répartition des sièges d’un parlement aux différents partis d’un Etat en fonction du nombre de voix accordées à chacun d’eux. Donc cette loi est un algorithme transformant le nombre de votes exprimés par les citoyens pour un parti en nombre de sièges assignés au même parti.
Dans un Etat, on a N électeurs et K partis en compétition, appélés P1, P2,…, Pk. Soit vi le nombre de votes pour le parti Pi (on suppose qu’il n’y a pas de bulletin nul ou blanc). Donc v1+v2+…+vk = N. On note S le nombre de sièges qui compose le parlement. La loi électorale établit le nombre de sièges Si à assigner au parti Pi en fonction de ses votes vi (S1 sièges pour le parti P1 etc…). On doit avoir S1+S2+…+Sk = S. Le nombre de sièges assignés à un parti est «proportionnel» aux votes. La formule mathématique pour le calcul de Si est Si = vi * S/N. Ce nombre est rarement un entier. La loi doit donner une indication précise pour le calcul du nombre entier de sièges Si. Certains seront tentés par un arrondi à l’entier supérieur si le chiffre situé à droite de la virgule est supérieur ou égal à 5 (exemple : 5.7 sera arrondi à 6) et un arrondi à l’entier inférieur si ce chiffre est strictement inférieur à 5 (exemple : 3.45 sera arrondi à 3). Malheureusement, il n’est pas dit qu’on arrive, à la fin, au nombre de sièges S en additionnant S1+S2+…+Sk.
Un exemple simple: On suppose N=1000 nombre total d’électeurs, k=3 partis et S=10 sièges
| CAS 1 | Votes Vi | Siège théorique vi * S/N | Sièges Si (arrondi supérieur) |
| Parti P1 | 680 | 6.8 | 7 |
| Parti P2 | 260 | 2.6 | 3 |
| Parti P3 | 60 | 0.6 | 1 |
| TOTAUX | 1000 | 10 | 11 |
| CAS 2 | Votes Vi | Siège théorique vi * S/N | Sièges Si (arrondi supérieur) |
| Parti P1 | 530 | 5.3 | 5 |
| Parti P2 | 330 | 3.3 | 3 |
| Parti P3 | 140 | 1.4 | 1 |
| TOTAUX | 1000 | 10 | 9 |
Dans le cas 1, il faudrait un siège en plus au Parlement, alors que dans le cas 2, un siège restera vide ! Ce mode de calcul de la proportionnelle n’est pas toujours fiable et il n’est pas toujours simple de faire respecter la proportionnalité.
Des algorithmes ont été proposés pour assigner à un parti un nombre de sièges qui est une approximation de son quota théorique « observé ».
1- L'algorithme H (ou Hamilton) ou des plus grands restes
C’est un algorithme facile à exploiter mais peut conduire à des paradoxes. En première étape, on calcule les sièges théoriques vi * S/N pour assigner à chaque parti Pi les sièges sûrs par l’arrondi à l’entier inférieur (exemple: 5.7 sera arrondi à 5, de même 1.4 sera arrondi à 1). Si tous les sièges sont assignés c’est fini, sinon on calcule les «restes» qui seront classés par ordre décroissant. On termine par assigner un siège de plus à tous les premiers partis de cette liste de «restes» ordonnés, jusqu’à obtenir un nombre total S des sièges assignés. En cas d’égalité de deux «restes» (situation rare !) on attribue un siège de plus à celui des partis qui a obtenu le plus grand chiffre devant la virgule.
Simulation avec les données précédentes: N=1000, S=10 sièges
| CAS 1 | Votes Vi | Sièges théoriques | Sièges sûrs | «Restes» | Sièges additionnels | Total des Sièges |
| Parti P1 | 680 | 6.8 | 6 | 0.8 | 1 | 7 |
| Parti P2 | 260 | 2.6 | 2 | 0.6 | 1 | 3 |
| Parti P3 | 60 | 0.6 | 0 | 0.6 | 0 | 0 |
| TOTAUX | 1000 | 10 | 8 |
| 2 | 10 |
| CAS 2 | Votes Vi | Sièges théoriques | Sièges sûrs | «Restes» | Sièges additionnels | Total des Sièges |
| Parti P1 | 530 | 5.3 | 5 | 0.3 | 0 | 5 |
| Parti P2 | 330 | 3.3 | 3 | 0.3 | 0 | 3 |
| Parti P3 | 140 | 1.4 | 1 | 0.4 | 1 | 2 |
| TOTAUX | 1000 | 10 | 9 |
| 1 | 10 |
On constate que tous les sièges ont été assignés aux différents partis selon le nombre de votants en leur faveur. Mais même l’algorithme H n’est pas convaincant, car il peut donner des résultats paradoxaux pour diverses élections successives. Elle présente le défaut de fournir des résultats parfois incohérents comme le montre le paradoxe de l’Alabama(1) et le paradoxe de l’Oklahoma(2).
Remarque: certains utilisent le quotient électoral (QE), qui est égal à QE= N/S (dans notre exemple, QE=1000/10= 100), pour calculer le nombre de sièges sûrs :en prenant l’arrondi à l’entier inférieur du résultat de la division de vi par QE. Ensuite on calcule le «reste» des voix en les classant par ordre décroissant et on assigne un siège aux premiers partis de cette liste ordonnée jusqu’à avoir un total S. Dans notre exemple, pour le parti P1, 680/QE = 680/100=6.8 donc 6 sièges sûrs, le reste sera égal à 680-6*100 = 680-600 = 80. Ce calcul avec le QE donne un résultat identique du tableau précédent.
2- L'algorithme J
L’algorithme J (comme Jefferson) a été proposé pour améliorer l’algorithme H. Il est prouvé que cet algorithme ne présente pas ni le paradoxe d’Alabama, ni celui de l’Aklahoma. On utilise le quotient électoral (QE). La première répartition s'effectue exactement de la même manière qu'avec la méthode des plus forts restes. Pour le premier siège additionnel, les scores de chacune des listes sont divisés par leur nombre de sièges plus un.Les résultats sont comparés et le siège va à la liste au quotient le plus élevé (la plus forte moyenne). Pour le deuxième siège additionnel, la même méthode est appliquée mais le score de chaque liste est divisé par son nombre de sièges augmenté de deux, et non plus d’un. Les calculs se poursuivent jusqu’à ce que plus aucun siège ne soit à attribuer.
Illustration : N=1000 (nombre de voix exprimés) et S=5 sièges (nombre de sièges à gagner). Ici le quotient électoral est QE= 1000/5=200
| CAS 1 | Votes Vi | Vi/QE | SS | Premier Vi/(SS+1) | SS | Deuxième Vi/(SS+1) | Répartition des Sièges |
| Parti P1 | 680 | 3.4 | 3 | 170(*) | 4 | - | 4 |
| Parti P2 | 260 | 1.3 | 1 | 130 | 1 | - | 1 |
| Parti P3 | 60 | 0.3 | 0 | 60 | 0 | - | 0 |
| TOTAUX | 1000 | 5 | 4 |
| 5 |
| 5 |
| CAS 2 | Votes Vi | Vi/QE | SS | Premier Vi/(SS+1) | SS | Deuxième Vi/(SS+1) | Répartition des Sièges |
| Parti P1 | 530 | 2.65 | 2 | 176.6(*) | 3 | 132.5 | 3 |
| Parti P2 | 330 | 1.65 | 1 | 165 | 1 | 165(*) | 2 |
| Parti P3 | 140 | 0.7 | 0 | 140 | 0 | 140 | 0 |
| TOTAUX | 1000 | 10 | 3 |
| 4 |
| 5 |
(*) Correspond à la plus forte moyenne de l’étape de calcul.
La répartition de sièges est donc :dans CAS 1, 4 sièges pour P1, 1 siège pour P2 et 0 siège pour P3; dans CAS 2 P1 ne gagne plus que 3 sièges alors que P2 ont aura 2 sièges et toujours 0 siège pour P3.
En Europe, la méthode d’Hondt est une version de la «plus forte moyenne» plus utilisée que l’algorithme J.
3- La méthode D’Hondt ou de «la plus forte moyenne»:
Le principe est simple : on fait le rapport entre le nombre de voix et le nombre de siège, et on prend les meilleures moyennes.En divisant par 1, puis par 2, puis par 3, etc. le nombre de suffrages obtenus par chaque liste, on obtient une série de quotients, que l’on peut classer par ordre décroissant. Ces quotients servent à déterminer le nombre de sièges revenant à chaque formation, au prorata du poids de chacune d’entre elles.
Illustration : N=1000 (nombre de voix exprimés) et S=5 sièges(nombre de sièges à gagner).
| CAS 1 | Vi/1 | Vi/2 | Vi/3 | Vi/4 | Vi/5 | Nombre de sièges |
| Parti P1 | 680(1) | 340(2) | 226.6(4) | 170(5) | 136 | 4 |
| Parti P2 | 260(3) | 130 | 86.6 | 65 | 52 | 1 |
| Parti P3 | 60 | 30 | 20 | 15 | 12 | 0 |
| CAS 2 | Vi/1 | Vi/2 | Vi/3 | Vi/4 | Vi/5 |
|
| Parti P1 | 530(1) | 265(3) | 176.6(4) | 132.5 | 106 | 3 |
| Parti P2 | 330(2) | 165(5) | 110 | 82.5 | 66 | 2 |
| Parti P3 | 140 | 70 | 46.6 | 35 | 28 | 0 |
Entre parenthèse le numéro d’apparition au sein de la liste des quotients rangés par valeur décroissante.
Le Sième nombre de cette liste ordonnée est appelé le diviseur électoral qui sera noté D. Pour le Cas 1 le diviseur électoral est D=170 et pour Cas 2 il est de 165. On voit que la ième liste se voit attribuer le nombre de sièges égal au nombre entier de fois que le diviseur électoral D se trouve dans vi. Par exemple dans le Cas 2 avec D=165, la liste du parti P2 aura 330/165=2 sièges, le parti P1 aura 530/165=3,21..soit3 sièges et le parti P3 aura 140/165=0.848… soit 0 siège.
La méthode d'Hondt est utilisée en Australie, en Finlande, en Pologne, au Portugal, en Espagne et aux élections législatives et régionales de Belgique. Elle est aussi utilisée en France pour les élections Européennes. Elle a la particularité d'avantager les listes ayant bénéficié du plus grand nombre de voix.
Une variante de cette méthode est la méthode de Sainte-Laguë. Dans les systèmes de Sainte-Laguë et de Sainte-Laguë modifié, les diviseurs sont différents de ceux utilisés dans le système de d'Hondt. Dans le système de Sainte-Laguë, on divise les votes que recueille un parti par 1, 3, 5, 7 etc., plutôt que par 1, 2, 3, 4... Plusieurs pays scandinaves ont recours à version modifiée de ce système, dans laquelle le premier diviseur est établi à 1.4 au lieu de 1 (si bien que les diviseurs sont alors 1.4, 3, 5, 7, etc.). Dans un système multipartite, les formations de taille moyenne ont alors tendance à être favorisées.
| CAS 1 | Vi | Vi/1.4 | Vi/3 | Vi/5 | Nombre de sièges |
| Parti P1 | 680 | 485.7(1) | 226.6(2) | 136(4) | 3 |
| Parti P2 | 260 | 185.7(3) | 86.6(5) | 52 | 2 |
| Parti P3 | 60 | 42.8 | 20 | 12 | 0 |
| CAS 2 | Vi | Vi/1.4 | Vi/3 | Vi/5 |
|
| Parti P1 | 530 | 378.5(1) | 176.6(3) | 106(5) | 3 |
| Parti P2 | 330 | 235.7(2) | 110(4) | 66 | 2 |
| Parti P3 | 140 | 100 | 46.6 | 28 | 0 |
La méthode de Sainte-Laguëmodifiée est utilisée en Allemagne (avec placement d’un seuil électoral), Bosnie-Herzégovine, Norvège, Nouvelle-Zélande, Suède, Danemark.
4- Le découpage électoral
Périodiquement, pour des raisons démographiques, il est indispensable de modifier les découpages pour que les circonscriptions «collent» avec l’évolution de la population. En pratique, ces modifications peuvent être l’occasion de réduire le nombre d’adversaires élus et/ou favoriser une représentation accrue à certaines catégories de populations ou bien tel ou tel «lobby». Le découpage pour favoriser un camp, est de chercher, chaque fois que cela est possible, à déplacer le nombre des élus en faveur de ce camp, au détriment du camp adverse.
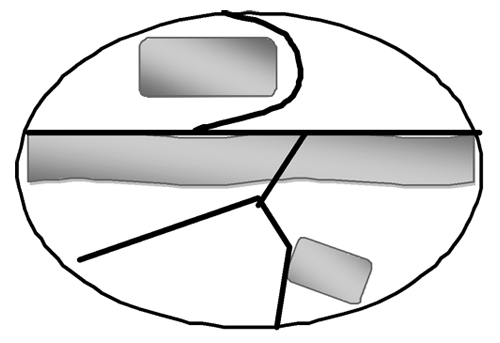
Pour illustrer nos propos, nous présentons deux exemples: le premier exemple est un dessin qui représente une région (gouvernorat, par exemple) découpée en cinq circonscriptions: en gris, les zones de forte influence du camp que l’on veut favoriser, en blanc les zones où ce camp est minoritaire. Avec l’hypothèse d’un siège par circonscription, ce découpage donnera au camp que l’on veut favoriser trois des cinq sièges.
Le deuxième exempleest un tableau indiquantles votes de trois partis P1, P2 et P3 ventilés sur six bureaux qui définissent trois circonscriptions A+D, C+E et B+F
|
| P1 | P2 | P3 |
| Bureau A | 1170 | 1340 | 820 |
| Bureau B | 1180 | 820 | 970 |
| Bureau C | 830 | 500 | 1050 |
| Bureau D | 1270 | 1580 | 660 |
| Bureau E | 950 | 1060 | 680 |
| Bureau F | 760 | 1220 | 880 |
Le parti P1 gagne un siège sur la circonscription regroupant les bureaux C et E (circonscription C+E) ; de même P2 gagne deux sièges dans les circonscriptions A+D et B+F.
Changeons le découpage : par regroupement de différents bureaux on modifie les circonscriptions. On crée les circonscriptions suivantes : A+B, C+D et E+F. Avec les mêmes votes on constate que P1 obtiendra deux sièges contre un seul à P2. Si les circonscriptions étaient B+C, A+E et D+F, cette fois, P3 gagnerait un siège tandis que P1 n’en aurait plus!
En regroupant différemment certains bureaux de vote en nouvelles circonscriptions on peut favoriser un camp sur un autre.
L'exemple du découpage de la ville de Paris
En 1986, le ministre de l'Intérieur français de l'époque, confia à un de ses conseillers, Alexandre Baetche, professeur à la Sorbonne et adjoint au maire du 5ème arrondissement, le redécoupage des circonscriptions de Paris en vue des prochaines élections législatives. Il devrait prendre en compte quatre contraintes. La première était d'ordre démographique : il fallait répartir 2,2 millions d'électeurs sur 21 circonscriptions (un député par circonscription de 105000 électeurs avec une variation de 10%), avec une réduction du nombre de bureaux de vote. La deuxième consistait à ne pas «révolutionner» la répartition précédente en sauvegardant, dans la mesure du possible, l'intégrité des quartiers et des arrondissements. La troisième est que le projet soit suffisamment cohérent pour être avalisé. Et enfin la quatrième contrainte était d'être le plus favorable possible au parti RPR (de Droite) de l'époque, sans ressembler ouvertement à un «charcutage». Grâce à ce redécoupage la Droite a remporté de nombreuses circonscriptions supplémentaires aux législatives de 1988.
Pour accomplir ce travail, il s'est basé sur des statistiques assez fines fournies par le ministère de l'Intérieur et l'INSEE (Institut National de la Statistique et des Etudes Economiques) sur le nombre d'habitants et des résultats complets des cinq dernières élections. Des techniques mathématiques ont permis de faire des projections sur l'évolution des votes bureau de vote par bureau de vote. La connaissance du terrain et le sens «politique» étaient indispensables pour être le plus fiable possible concernant la quatrième contrainte (avantage à donner au mouvement RPR). Ce redécoupage restait en vigueur jusqu'en juin 2012. Ce dernier découpage, en 18 circonscriptions au lieu de 21, tenait compte de l’évolution de la population parisienne et du nombre total de députés (un député par circonscription d’environ 125000 électeurs).
5- Conclusions
Contrairement aux systèmes majoritaires, qui favorisent la formation de gouvernements formés d'un seul parti, les systèmes «proportionnels» donnent généralement naissance à des gouvernements de coalition qui sont jugés moins stables que les gouvernements majoritaires.
Ainsi, il n’y a pas de mode de scrutin «proportionnel» parfait. Avec la méthode de «plus fort reste», on peut gagner des voix et perdre un siège! En plus la multitude de groupes instables serait impropre à dégager une «majorité» nette et durable sur un programme, et le pays risque d’être ingouvernable à cause de renversements possibles des jeux d’alliances et de «tourisme partisan». La méthode de la «plus forte moyenne» reste un système plus équitable et dégage, en général, un gouvernement plus stable, donc un pays gouvernable.
Pour éviter une multiplication excessive du nombre des partis, certains pays fixent parfois un seuil quant au nombre de voix que les partis doivent réunir pour obtenir des sièges. Ces seuils varient d'un pays à l'autre. Par exemple, en Allemagne, les partis doivent recueillir au moins 5% des suffrages exprimés (l'établissement de seuils élevés visait à éviter l'apparition de petits partis extrémistes).
Enfin, le découpage électoral constitue un enjeu majeur. Il est en partie certainement stratégique.
Salaheddine Maïza
(*)Docteur en Statistiques et ancien auditeur C.E.D.S-Paris
(1) http://fr.wikipedia.org/wiki/Paradoxe_de_l%27Alabama
(2) paradoxe de l’Oklahoma : il apparut quand cet état a rejoint les États-Unis, en 1907.
À cette époque, le Congrès comptait 386 sièges, répartis entre les états selon le recensement de 1900, lequel dénombrait 74562608 habitants au total. Chaque siège devant donc représenter 193167 personnes et en estimant à environ un million le nombre d’habitants de l’Oklahoma, le nombre de sièges fut augmenté de 5, passant de 386 à 391. L’application de la méthode de Hamilton après l’entrée de l’Oklahoma dans les États-Unis aurait bien attribué les 5 nouveaux sièges à l’Oklahoma mais, à la surprise des employés du Bureau de recensement se livrant à ces simulations, l’état de New York (7264183 habitants) aurait été obligé de donner un de ses 38 sièges au Maine (694466 habitants), alors que leurs populations (ainsi que celles des autres états) étaient supposées inchangées.
Références:
a/ Magasine Tangente, n°45, Hors Série
b/ Les systèmes électoraux, B O'Neal, Mai 1993
c/ http://fr.wikipedia.org/wiki/Scrutin_proportionnel_plurinominal
- Ecrire un commentaire
- Commenter

Y a une petite erreur de somme au niveau du point 2 aussi vous avez changé de total de Sièges à 5... Sinon vraiment merci pour votre article il est très enrichissant :)

.jpg)




























